Solo tú puedes ver tu arcoíris.

El arcoíris es uno de los espectáculos visuales más bellos que puede ofrecernos la naturaleza junto a auroras boreales o tormentas eléctricas. Este fenómeno ha acompañado al ser humano desde su origen pero la falta de conocimientos físicos y matemáticos solían acabar atribuyendo su existencia a una causa divina.

Aristóteles, allá por el 340 a.C. (no hay consenso sobre la fecha exacta), postuló que lejos de ser una entidad material era una suerte de reflexión de la luz solar debida a las nubes que formaba un cono con la visual del observador. En 1266 Roger Bacon, filósofo, científico y teólogo franciscano alcanzó a medir el ángulo que forman los rayos de luz solar incidentes y los refractados que forman el arcoíris definiendo lo que se conoce como ángulo del arcoíris.

El dominico alemán Thierry de Friboug postuló hacia al año 1300 que el arcoíris no se producía como una única pieza visual  sino que cada gota de agua era capaz de crear un minúsculo arcoíris y que la acumulación de las mismas creaban una densidad tal que conferían la forma y aspecto final. No deja de resultar sorprendente esta correcta deducción para la época porque, además, pone de manifiesto un hecho del que no solemos percatarnos como es que, cada cual, ve su propio arcoíris dado que la observación depende del ángulo y distancia de nuestra visual.

Ya podemos intuir que tienen que coexistir dos elementos fundamentales para que el arcoíris pueda componerse: la luz solar, que siempre quedará a espaldas del observador (de otra forma sería difícil encontrar alguna fotografía donde aparezca) y el agua en forma de gotas. 

Detengámonos un instante y formemos una gota de líquido en nuestra mente. En ausencia de fuerzas externas nuestro líquido estará sometido a las fuerzas de cohesión de las moléculas que componen su estructura que presentan mayores efectos en la frontera que en su interior. A esto se le conoce como tensión superficial y podríamos identificarlo con una especie de lámina muy delgada y elástica que envuelve al líquido y que, en ausencia de otras fuerzas externas, tiende a procurar un estado de mínima energía que es capaz de conseguir cuando la tensión es idéntica en todos sus puntos. Esto ocurre cuando adopta una forma esférica. Ahora bien, cuando una gota cae, se acelera por efecto de la gravedad en función de su masa interviniendo la segunda Ley de Newton pero en ese sumatorio de fuerzas donde aparecerá el peso de la gota también influye la fuerza creada por el rozamiento con el aire que es proporcional a la velocidad (a más velocidad, más rozamiento hasta llegar a una velocidad límite) provocando que la gota adopte una forma esferoide que no llega a ser tan dramática como solemos ver representada en numerosos dibujos a modo de lágrima. Así la cosa, deberán darse unas condiciones de forma de gota y de condiciones ambientales (densidad del aire, humedad…) que faciliten la esfericidad de la gota para disfrutar de este espectáculo visual.

Antonio de Demini, Descartes y el mismísimo Newton forman parte del elenco de científicos y pensadores que estudiaron el arcoíris en busca de una explicación racional siendo este último quien logró descomponer la luz blanca del sol en distintos haces de color en función de su longitud de onda cuando atravesaba la estructura de un prisma.

Cuando un rayo incide sobre una gota se producen dos tipos de interacciones entre la luz y el medio (sea este el aire o el agua). El primer efecto es la reflexión que permite al haz luminoso “rebotar” sobre la superficie del medio con una simetría perfecta entre la incidencia y la reflexión. Por otro lado el haz, al cambiar de medio, altera su dirección en función de cómo modifique su velocidad (atención a esto porque la velocidad de la luz cambia con el medio en el que se propaga). Así, el cociente entre la velocidad de la luz en el vacío (299 792 458 m/s) y en el agua (224 844 349 m/s) resulta ser 1.333 que corresponde al índice de refracción de esta medio líquido. Según Willebrord Snell, los senos de los ángulos de incidencia y de refracción para dos medios (aire/agua en nuestro caso) estarán en relación constante e igual al cociente de sus respectivos índices de refracción.

Cuando un rayo incide sobre una gota esférica puede hacerlo en la línea que une el foco de luz (para nosotros el sol) con el centro de la gota o separándose del centro en una distancia no mayor a su radio, ya sea sobre el eje o bajo él. A esta distancia se denomina “parámetro de impacto” y es decisivo a la hora de estudiar cómo se producen las interacciones del rayo con cada medio en los distintos impactos que efectúa contra cada uno. Supongamos el caso de una gota esférica de agua y analicemos los primeros movimientos.

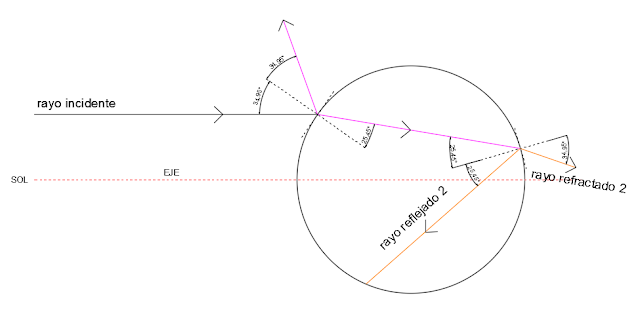
El rayo proveniente del sol se dirige “casi” paralelo al eje de la gota dado que la distancia de esta a aquel es tan grande que casi se trataría de una distancia infinita y, como sabemos, el infinito corresponde al lugar donde se cortarían dos paralelas. Al alcanzar la gota una parte se reflejaría (rayo reflejado 1) de forma simétrica con respecto a un plano perpendicular al plano tangente a la gota en el punto de impacto. Otra parte del rayo se refractaría (rayo refractado 1) al cambiar de medio según la Ley de Snell hasta que alcanzara la siguiente frontera de líquido en su cara interna.

Ahora se ha producido un nuevo reflejo que da lugar al rayo reflejado 2 y una refracción donde ahora el rayo, con menor intensidad, abandona el medio acuoso para dirigirse, de nuevo, al aéreo.

Es ahora el rayo refractado 3 o de tercer orden el encargado de formar el arcoíris primario tras la segunda reflexión. Mientras, nuevamente, el rayo reflejado 3 alcanza la frontera de líquido en la cara interna de la gota produciéndose sendas reflexiones y refracciones. 

Este rayo reflejado 3 da lugar al rayo reflejado 4 y sería el rayo refractado 4 o de cuarto orden el que provocaría el conocido como arcoíris secundario y es que los arcoíris no se forman de manera aislada lo que ocurre es que su intensidad lumínica puede afectar a su percepción por el observador. A partir de aquí se producirían rayos de órdenes superiores que difícilmente alcanzan a ser visibles por la pérdida energética del haz y darán lugar a lo que se conoce como arcos supernumerarios.

Conforme el parámetro de impacto crece y el rayo incidente se aleja del eje central el ángulo de desviación se reduce. El límite lo encontramos en los rayos tangentes donde el parámetro de impacto alcanza el radio de la gota. De hecho, el ángulo de desviación cae hasta un mínimo que se corresponde con 138º cuando este parámetro alcanza aproximadamente ⅞ del radio de la gota y vuelve aumentar nuevamente. A este rayo se le conoce con un nombre propio, el “rayo del arcoíris”. He aquí una primera consecuencia. Será con 42º de inclinación como deberemos mirar hacia las gotas de agua que producirán el arcoíris para ser capaces de verlo. 

En el caso de los rayos de cuarto orden, cuando el parámetro de impacto es nulo, también se anula su ángulo de desviación ya que los rayos “rebotan” dos veces en el eje diametral de la gota y continúan su marcha en medio aéreo. 

En estos rayos de cuarto orden, el incremento del parámetro lleva asociado un máximo del ángulo de desviación en lugar de un mínimo que se corresponde con 130º y luego decrece.

Cuando la gota está uniformemente iluminada, los parámetros de impacto barren toda la gota creándose acumulaciones de rayos en el entorno de los rayos refractados 3 y 4. La intensidad que puede encontrarse entre los 138º del rayo de tercer orden y los 130º del de cuarto es casi nula por lo que se produce una banda oscura que se denomina “banda de Alejandro”. En este punto Descartes ya apuntó un problema y es que la banda no es negra sino oscura y ello es porque deben existir arcoíris de órdenes superiores que de algún modo aporten luminosidad a dicha franja. Conforme a la teoría cartesiana, el tamaño de la gota no es algo a tener en cuenta ya que depende de su forma no del radio como se demuestra en los experimentos que el propio Descartes realizó en ampollas esféricas de vidrio llenas de agua pero sí resulta un factor clave en la justificación ondulatoria.

Atendiendo a la variedad cromática del arcoíris aprovecharemos lo que Newton descubrió cuando estudió cómo la luz atravesaba los prismas. La luz blanca es una mezcla cromática que proviene de la yuxtaposición de diferentes colores, cada uno de los cuales, presenta una longitud de onda propia y un diferente índice de refracción por propagarse en el medio a distinta velocidad. Volviendo al análisis que ya hemos realizado podríamos decir que cada color de los que se compone la luz blanca refractaría en una banda distinta a sus coaligados

Lo que Newton fue capaz de calcular usando la geometría era que la luz roja tenía un ángulo de desviación sobre el plano de horizonte de 137º 58’ mientras que la luz violeta desviaba su rayo a razón de 139º 43’. Dado que estos son los colores extremos de la franja arcoíris, obtuvo que la anchura de un arcoíris se corresponde con la diferencia entre ambos (1º 45’) siempre que se consideren rayos paralelos. En realidad esto no ocurre pues el diámetro que se aprecia del Sol desde la Tierra puede considerarse 32’ (aproximadamente 0.53 grados de arco) que corrige el anterior valor a 2º 15’.

Hasta aquí, hemos visto cómo se forma un arcoíris a partir de la óptica geométrica pero, como habíamos adelantado, existía un problema a la hora de dar explicación a la banda oscura de Alejandro que crean los arcos de órdenes superiores.  La luz es una onda y como tal depende de su longitud de onda que mide la distancia real que recorre la misma en un tiempo dado. Thomas Young demostró que la luz podía crear interferencias por lo que, dependiendo del camino que cada rayo de luz escoja para circular (más cerca o más alejado del eje), se crearán zonas de interferencia constructiva (las ondas se suman creando zonas brillantes) o zonas de interferencia destructiva (las ondas se restan y anulan creando zonas oscuras). Aquí, por tanto, el camino es una variable a tener en consideración (no como vimos en las consideraciones cartesianas) y el tamaño de la gota es crucial. Cuando el haz luminoso recorre gotas pequeñas (menores a 1 mm) apenas se crean interferencias destructivas pero sí se encuentran si las gotas son mayores (cosa que ocurre al aglutinarse gotas entre sí por causa de su tensión superficial cuando caen).

Ahora el tema se complica conceptual y cuantitativamente porque el fenómeno de difracción lleva asociado una manifestación ondulatoria donde la luz parece curvarse cuando se aproxima a un obstáculo pero, claro, en el borde de un arcoíris, no existe este obstáculo físico. ¿Por qué, entonces, se produce este decaimiento cromático? Hay que prestar atención al descubrimiento del químico y físico Richard Potter quien acuñó por vez primera el término de “línea cáustica” para definir la envolvente de un sistema de rayos y resulta de interés el entorno del rayo refractado que causa el arcoíris primario. Estudiar la distribución de esta familia de rayos requiere de más enjundia matemática y física por requerir estudios de Huygens y Fresnel sobre difracción pero avancemos unas pinceladas que nos permitan recorrer de puntillas esta teoría. Un teorema conocido como de Fresnel-Kirchoff permite recomponer un frente de onda conociendo las amplitudes de las mismas y su distribución. Este hecho sirvió al astrónomo y matemático inglés George Biddell Airy, quien partió de un frente de ondas restringido geométricamente y con amplitudes basadas en hipótesis de la teoría de difracción, para obtener una expresión matemática, una función integral conocida como “función de Airy”, que representaba la intensidad de la luz desviada en la región del arcoíris.

Tanto Descartes como Thomas Young alcanzaron a coincidir en que para el ángulo de mínima desviación se produce una intensidad infinita por efecto de la presencia de la “línea cáustica” y por ello se representa con un valor asintótico vertical en la frontera pero con la herramienta matemática de Airy no es posible alcanzar en ningún lugar un valor infinito. Con respecto al decaimiento de la intensidad luminosa la teoría de Airy prevé una disminución progresiva al adentrarnos en la banda oscura lo que concuerda con la teoría de difracción y la naturaleza ondulatoria de la luz. Ahora bien, Airy realizó sus cálculos en base a un supuesto arcoíris monocromático por lo que su extrapolación al caso real supondría superponer las distribuciones de intensidad de Airy que se generan en cada componente cromática aislada.

Si has llegado al final del artículo, enhorabuena, tu afán de conocimiento ha superado a la tentación de sucumbir ante las teorías físicas y matemáticas que rodean a este fabuloso fenómeno natural. El mundo que nos rodea está repleto de causas místicas para el ignorante, de preguntas para el investigador y de respuestas para quienes están dispuestos a escuchar. 

Autor: Prof. Javier Luque.

Fuentes e Imágenes:

-          Divulgameteo / H. Moysés Nussenzveig

-          Dpto Física Aplicada ETSII UPM / Mecfunnet

-          Historical Encyclopedia of Natural & Mathematical Sciences

-          Wikibooks

-          El Arco Iris ¿Es un tratado de física? José Antonio Martínez Pons. Departamento de Química Analítica e Ingeniería Química UCM y Carlos Martínez Pons (A.E.N.A.)

-          Physics of rainbow Masatsugu Sei Suzuki. Binghamton University